Le Château de Versailles invite Hiroshi Sugimoto, du 16 octobre au 17 février. L’artiste japonais investira les jardins du domaine de Trianon où il conviera art, architecture et spectacle vivant.

Au printemps 2017, lors d’une journée à Château Lacoste près d’Aix-en-Provence, malgré une météo épouvantable, je suis tombé en arrêt devant cette pointe géante. À l’époque, je ne connaissais pas Hiroshi Sugimoto, le créateur de ce qui était donc à mes yeux, une pointe géante en aluminium. Ignorant son projet initialement consacré à la matérialisation artistique d’objets mathématiques, j’ai regardé cette œuvre en physicien.

D’une pointe géante en aluminium aux micropointes en silicium des nanos

À Grenoble, dans les laboratoires, l’utilisation de pointes à la forme très proche de celle produite par Ishori Sugimoto est quasi industrielle. Quelques « petites différences » bien sûr : d’abord, les pointes en silicium monocristallin des nanotechnologies sont des micropointes. Il faut passer du micromètre au mètre pour les comparer, soit un rapport d’un million tout de même. Ensuite, elles n’ont aucune autre visée que leur utilisation comme nanopalpeurs, c’est-à-dire comme des bâtons d’aveugle, jusqu’à l’échelle atomique pour explorer les surfaces de pratiquement tous les matériaux.

Mais il reste surprenant de voir combien leurs formes si peu naturelles sont proches. En fait, comme le but chez cet artiste est de nous montrer une forme mathématique idéale au moins pour notre perception, il aurait probablement même été plus simple pour lui de la produire à l’échelle micrométrique dans une salle blanche équipée pour produire des microstructures en silicium. C’est une vue de l’esprit bien sûr car pour voir ainsi ces micropointes, il ne faut rien moins qu’un microscope électronique à balayage. Pas simple à exposer dans un bassin rempli d’eau et en plein air.

« Le désir de donner corps à des idées géométriques »

Hiroshi Sugimoto explique clairement ses intentions :

« Newton a été le précurseur dans la poursuite de divers principes mathématiques, et de nombreux domaines des sciences naturelles ont depuis suivi ses traces. Au cours du XIXᵉ siècle et au début du XXᵉ siècle, le désir de donner corps à des idées géométriques a conduit à la création de modèles mathématiques, imaginés par des mathématiciens et sculptés à la main dans du plâtre par des artisans. J’ai essayé de transformer des équations mathématiques en objets tangibles en introduisant les équations dans un ordinateur et, en utilisant les outils d’usinage les plus avancés du Japon, je les ai produites en aluminium pur. »

Un artiste, un mathématicien et un technicien… ou la sculpture de formes complexes réinventée par les techniques de l’usinage numérique.

« Les matheux ne négocient jamais. »

Quel que soit votre niveau en maths, vous avez dû être saisi par une idée clé de cette partie de la science : « les matheux ne négocient jamais. » C’est juste ou faux. Il n’y a pas de milieu. Les surfaces des sculptures présentées dans la vidéo ci-dessus sont décrites par des équations que le New York Times a même publié avec les images des sculptures.

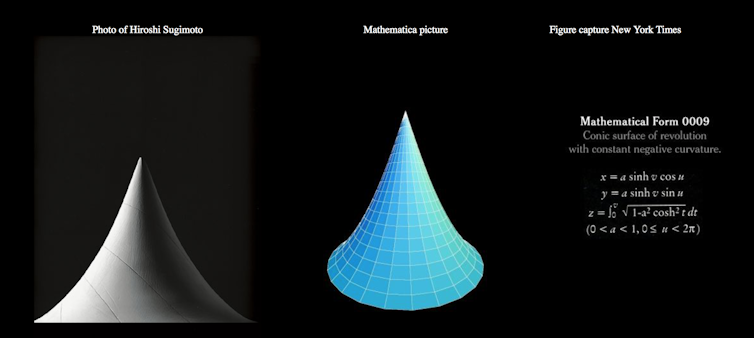
Comme le souligne cette capture d’écran issue d’un cours d’algèbre linéaire et d’équations différentielles de l’Université de Harvard, ces équations déterminent de manière idéale, parfaite la position de chaque point de coordonnées (x,y,z) dans un espace mathématique. Sans aucune approximation. Quels que soient les moyens mis en œuvre, aucune des sculptures matérialisant cette surface ne peut atteindre cet absolu pensé. Deux modèles réels de la même surface ne peuvent pas être identiques. Les physiciens sont justement capables de caractériser ces différences aussi petites soient elles. Matériellement, la perfection absolue de l’objet mathématique abstrait est hors de portée. Au demeurant, cela n’a aucune importance. Les représentations matérielles ne me semblent pas fondamentalement utiles en maths. Ni pour les définitions, ni pour énoncer des théorèmes, ni pour les démontrer. On peut toujours travailler, seul ou à plusieurs, avec des cercles tracés à la main sur des tableaux et sur le théorème de Pythagore avec des angles apparemment proches de 90°. Le message passe très bien ainsi.

Voir un objet mathématique et le rêver

Ishori Sugimoto ne peut donc pas atteindre cet absolu des mathématiques dans le monde réel. L’objet produit est bien déterminé par un ensemble d’équations mais il n’est pas idéalement fidèle. Il l’est seulement suffisamment pour satisfaire notre perception quand on le regarde. Ce « seulement » cache tout de même la difficulté de la réalisation. Notre perception est très performante. Dans les formes et sur les surfaces, elle détecte des défauts à un niveau tel que cette œuvre est réalisée « … en utilisant les outils d’usinage les plus avancés du Japon. » Dommage qu’on ne puisse pas la toucher. Malgré les performances incroyables de notre sens du toucher, son poli optique ne devrait pas nous permettre de détecter une quelconque rugosité.

En fait, s’il nous était permis de la toucher pour le constater par nous-mêmes, on ne sentirait qu’une surface lisse et douce sous la main. Dommage encore qu’on ne puisse pas l’écouter en collant dessus un capteur de vibrations comme l’accéléromètre d’un Smartphone. Ce son traduirait ses vibrations permanentes comme celles d’un instrument de musique, des déformations très petites, rapides et invisibles. Mais tout cela n’est évidemment pas accessible lors de la visite. Au contraire, le regardeur voit un objet très élégant, apparemment parfait, qui d’une part le rapproche de la perception qu’un scientifique peut avoir de cette surface, et d’autre part peut l’ouvrir à de multiples émotions propres à l’histoire de chacun, à l’endroit, à l’ambiance, aux amis présents…

L’incroyable rigidité de la matière

Je ne peux pas m’en empêcher : je regarde cette œuvre en physicien. Je vois une grande pointe en aluminium, proche des micropointes de silicium que je connais bien. Je ne suis donc pas d’abord sensible au propos de Hiroshi Sugimoto et au lien avec les mathématiques. Je crois que cette vision de physicien est première. Dans le cas des micropointes comme de l’œuvre de Sugimoto, il est en tous cas essentiel que nous ayons cette certitude que, quelques soient les circonstances, la forme ne changera pas… trop.

Change t-elle en réalité ? Oui et non. Les deux sont élastiques et vibrent en permanence. Les deux se dilatent ou se contractent selon les variations de température. Mais ces déformations sont très faibles. Dans le cas de la sculpture, nous ne le voyons pas. Dans le cas de la mesure avec les micropointes, cela n’altère pas le résultat. Dans les deux cas, ça marche donc très bien. Exceptionnellement bien d’ailleurs. La plupart du temps, nous n’y pensons même pas. Nous sommes trop habitués à l’extrême rigidité des matériaux comme l’acier, le verre ou le marbre. Cette rigidité définit parfaitement leur forme. Cette rigidité de la matière et son émergence nous sont des évidences. L’eau liquide n’est pas rigide. Elle est même infiniment déformable à notre échelle. Quand elle gèle, elle devient un solide très rigide.

Et alors ?

L’émergence de la rigidité selon Philip W. Anderson, prix Nobel de Physique

Alors je laisse la parole à Philip W. Anderson, Prix Nobel de Physique en 1977. Dans son livre intitulé « Basic notions in condensed matter », il a souligné il y a vingt ans son étonnement de physicien théoricien devant la rigidité d’une chaise que l’on peut bouger sans qu’elle ne se déforme :

« Nous sommes tellement habitués à la rigidité des corps solides – l’idée, par exemple, que lorsque nous déplaçons une extrémité d’une règle, l’autre extrémité se déplace sur la même distance – qu’il est difficile de réaliser qu’une telle action à distance n’apparaît pas explicitement dans les lois de la nature sauf dans le cas de forces à longue portée comme la gravité ou l’électrostatique… Nous sommes tellement habitués à cette propriété de rigidité que nous n’acceptons pas sa nature presque miraculeuse, qu’elle est une “propriété émergente” non contenue dans les lois simples de la physique, bien qu’elle en soit une conséquence. »

La physique peut nourrir cet étonnement élémentaire plus avant encore. Un verre à eau quelconque contient environ un nombre d’Avogadro d’atomes. Une mole. Poussez ce verre à la main comme il vous plaira, les quelques 6,10²³ atomes vont tous se déplacer ensemble, en même temps et exactement de la même distance. Dans le cadre du développement de l’instrumentation liée à la mesure des ondes gravitationnelles par exemple, mais aussi dans une multitude d’autres cas y compris lors de mesures pour des études fondamentales en physique quantique, cette propriété a été poussée dans ses retranchements. On a mesuré des déplacements considérablement plus petits que la taille d’un atome. Y compris pour des objets de taille macroscopique. À de multiples reprises.

Rigueur et absolu scientifiques peuvent nourrir notre liberté devant une œuvre. N’est elle pas réussie si elle conduit chacun à la rêver singulièrement ? L’historien d’art Daniel Arasse disait d’un tableau qu’il peut se lever mystérieusement devant le regardeur, ou pas. Voici donc comment, en physicien, j’ai rêvé cette œuvre de Hiroshi Sugimoto.

La version originale de cet article a été publiée sur The Conversation.