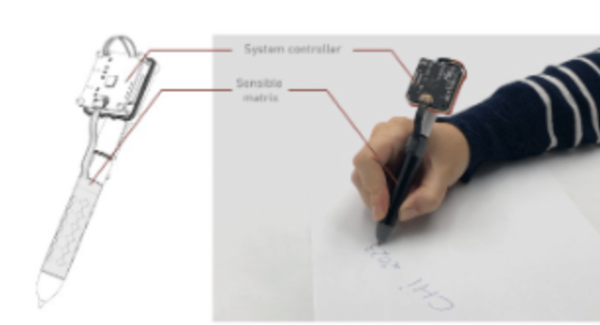
Dans Conceptual Forms, les œuvres de Hiroshi Sugimoto, exposées en 2004 à la Fondation Cartier pour l’art contemporain, on trouve aussi bien des modèles réels de formes mathématiques que des photos de systèmes d’engrenages comme celui que vous voyez ci-dessus. Car « Art resides even in things with no artistic intentions » (l’art réside même dans les choses dénuées d’intention aertistique), comme le dit Hiroshi Sugimoto. Après un premier article fondé d’une part sur l’œuvre de Hiroshi Sugimoto exposée au Château La Coste, d’autre part du texte de P.W. Anderson sur la rigidité dans la matière condensée, et enfin sur la vision de la pointe rigide, je suis tombé sur ses photos d’engrenages. On ne peut décidément pas tout prévoir. J’ai donc souhaité me pencher cette fois sur les systèmes d’engrenages chez Hiroshi Sugimoto, pour les mettre en rapport avec le voyage intuitif de François Dufour à travers les échelles de longueur, de notre échelle à celle du nanomonde, et avec la réflexion menée par P.W. Anderson, qui a illustré le concept de rigidité généralisée, justement avec des engrenages.

« Dix puissance moins neuf », une œuvre de François Dufour

Ici on voit, mais on doit aussi toucher et manipuler. L’un des exemplaires de cette œuvre est exposée dans la salle Nanomonde du CIME Nanotech à MINATEC Grenoble. L’œil et la main sont à l’œuvre ensemble. Cette machine est probablement un des meilleurs dispositifs pour permettre à notre perception de se confronter avec les changements d’échelles sans être immédiatement mise hors jeu. On bouge à notre échelle et l’effet se transmet idéalement directement à l’échelle nanométrique.

Le système est constitué de neuf disques associés chacun à un pignon. Le rapport entre disque et pignon est de dix. Quand le premier disque équipé d’une manivelle fait un tour, le second lié par frottement fait un dixième de tour. Le dernier un milliardième de tour. Chaque disque est associé à une lettre du mot « nanomètre » qui compte bien neuf lettres. Bien sûr, à nouveau, si cette idée est magnifique, en pratique, il est impossible à celui qui l’expérimente de faire tourner tous les disques. Il est même quasi impossible humainement de tester la machine complètement. Les disques sont liés entre eux par frottement. Y a-t-il quelque part du jeu dans la mécanique qui change tout ? A quel point ? Construire un dispositif qui transmet le mouvement de roue en roue de manière mesurable est en fait un problème d’instrumentation difficile. C’est pratiquement un sujet de recherche.

La « rigidité généralisée » selon P.W. Anderson, prix Nobel de physique

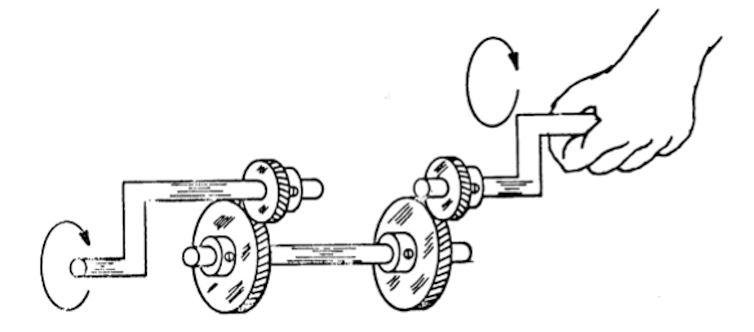
L’intuition étonnante de Francois Dufour et de ses élèves est éclairée et soulignée par le commentaire de P.W. Anderson associé à ce schéma :

« Illustration (quelque peu schématique) de la rigidité généralisée. Une force externe (la manivelle) se couple au paramètre d’ordre à une extrémité du système, représenté par un engrenage. Un changement de paramètre d’ordre à n’importe quel point du système est transmis à toutes les autres parties du système (le premier engrenage fait tourner le deuxième engrenage). Le deuxième engrenage fait tourner la deuxième manivelle : une force a été transmise d’une extrémité du système à l’autre par l’intermédiaire du paramètre d’ordre. »

J’ai gardé malgré tout, dans la traduction, l’expression extrêmement technique et très profonde en physique : « paramètre d’ordre ». Comme l’indiquent les flèches, on peut lire à la place « mise en rotation », « variation de l’angle de rotation ». L’idée essentielle ici véhiculée par l’idée de « rigidité généralisée » est qu’il impossible de faire tourner une manivelle sans que l’autre ne tourne aussi. Aussi petite que soit la rotation. De même, il n’est pas possible de déplacer une partie d’un solide sans le déplacer dans son ensemble, puisque il est rigide.

La rigidité, le changement d’échelles et les engrenages

La rigidité d’une pointe permet de manipuler sa base macroscopique pour bouger un atome à l’échelle nanométrique. La rigidité généralisée d’un système d’engrenages parfaits permet, dans la machine « Dix puissance moins neuf » de faire tourner le premier N attaché à la manivelle et d’obtenir immédiatement un milliardième de rotation du dernier E. Enfin en principe… mais en principe, c’est déjà beaucoup.

La version originale de cet article a été publiée sur The Conversation.