Article initialement publié en octobre 2018 sur The Conversation, en collaboration avec le blog Binaire.

Éric Blayo est professeur à l’Université de Grenoble Alpes où il est membre du Laboratoire Jean Kuntzmann. Il est membre de l’équipe AIRSEA après avoir dirigé pendant 10 ans l’équipe-projet commune MOISE (Inria-CNRS-UGA) Il s’intéresse à la modélisation mathématique et numérique des sciences de l’environnement (météo, système océan-atmosphère, climat). Ces processus complexes doivent selon lui faire l’objet de modélisation (éventuellement à plusieurs échelles de temps et d’espace) et d’assimilation de données qui permettent de corriger des modèles par essence toujours imparfaits. Pour Binaire, il nous parle ici de l’apport des big data dans son domaine de recherche.

La prévision météorologique fut un des tout premiers domaines scientifiques à faire usage de la simulation numérique : dès la fin des années 40 (première prévision numérique du temps par une équipe pilotée par Jule Charney et John Von Neumann en 1950), et même virtuellement 30 ans plus tôt dans les travaux visionnaires de Lewis Fry Richardson, qui en posait les bases et décrivait même ce que pourrait être une forecast factory (usine à prévision) météorologique. Depuis lors, des systèmes de prévision ont été développés progressivement pour toutes les sciences environnementales : météorologie, océanographie, pollution de l'air, hydraulique fluviale, climat… Mais alors, forts de décennies de travail et d'expérience, bénéficiant de la progression exponentielle de la puissance de calcul, alimentés par des quantités de données (notamment satellitaires) colossales, et maintenant baignés dans la révolution de l'intelligence artificielle, pourquoi ces systèmes numériques ne fournissent-ils pas encore des prévisions quasi parfaites ?

Un système de prévision, qu'est-ce que c'est ?

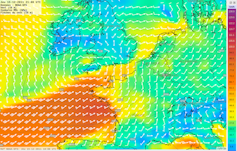
Pour tenter de comprendre cela, commençons par décrire ce qu'est un système de prévision dans ces domaines applicatifs. Avant tout, il est basé sur la connaissance de la physique des phénomènes mis en jeu. Ces lois physiques, qui traduisent en général des principes simples comme la conservation de la masse ou de l'énergie, sont exprimées sous forme d'équations mathématiques. Beaucoup sont d'ailleurs connues depuis les travaux de grands scientifiques comme Euler, Fourier, Navier, Stokes, Coriolis ou Boussinesq il y a deux siècles. Ces équations, qui mettent en jeu vitesse, pression, température, sont toutefois trop complexes pour être résolues exactement, et l'on va construire un modèle numérique afin de les résoudre de façon approchée (mais pas approximative !). Autrement dit, on remplace l'équation mathématique exacte par une expression approchée calculable par un ordinateur.

Mais, comme l'a dit Niels Bohr, physicien de génie et grand pourvoyeur de citations restées à la postérité : « Prévoir est très difficile, surtout lorsque cela concerne l'avenir ». Ainsi notre modèle numérique ne nous sera que de peu d'utilité pour prédire la situation de demain s'il n'est pas bien « calé », c'est-à-dire renseigné aussi précisément que possible sur la situation d'aujourd'hui : votre état de santé à l'issue d'une chute sera loin d'être le même suivant que vous trébuchez sur une plage de sable fin ou du haut d'une falaise de 30 mètres, et une connaissance parfaite de la loi de la gravitation n'y changera rien. Concrètement, cela signifie qu'il faut fixer les valeurs de toutes les variables du modèle à un instant donné, et donc utiliser pour cela les observations disponibles au même moment. Des techniques mathématiques très sophistiquées ont été développées pour cela, qu'on englobe sous le terme d'« assimilation de données ».

A ce stade, on dispose donc d'un système qui, utilisant les données sur l'état actuel, est capable de prédire un état futur. Pour parfaire le tout, on essaie même le plus souvent d'évaluer la fiabilité de cette prévision : c'est par exemple l'« indice de confiance » associé aux prévisions météo. Le montagnard, le marin, ou plus simplement le cycliste, connaît son importance, et fera des choix prudents si l'incertitude est grande. Cette incertitude est évaluée généralement par des techniques de « prévisions d'ensemble », consistant à réaliser de nombreuses prévisions en perturbant légèrement à chaque fois un paramètre du système, comme son état initial. Si les prévisions demeurent très cohérentes entre elles, alors on dira que la prévision est fiable ; si au contraire elles présentent des disparités fortes, on considérera que la prévision est incertaine.

Des erreurs, un papillon, et pourtant elle tourne !

Un système de prévision très précis serait synonyme d'une incertitude très faible dans toutes les situations possibles. Or, dans ce domaine des fluides géophysiques, il y a des erreurs significatives à tous les stades :

• dès les équations, déjà : on ne comprend pas toute la physique, et on la représente donc imparfaitement. La physique à l'intérieur des nuages par exemple est encore bien loin d'être parfaitement comprise.
• dans la partie numérique ensuite, qui par essence est une approximation. Incapable, même avec le meilleur ordinateur du monde, de calculer la solution approchée en tout lieu et à chaque instant, on va se contenter de le faire sur un maillage, c'est-à-dire en des points répartis géographiquement (les modèles numériques actuels en considèrent tout de même fréquemment la bagatelle de plusieurs dizaines ou centaines de millions). Ce faisant, on ne peut donc pas représenter ce qui se passe à des échelles plus petites que celle du maillage, et l'on va, soit choisir de l'ignorer totalement, soit tenter de simuler l'effet de ces petites échelles non représentées sur la solution : c'est ce que l'on appelle une « paramétrisation sous-maille », art extrêmement difficile.
• dans la description de l'existant enfin : on ne connait évidemment pas parfaitement la température actuelle en tout point de l'océan, ni la perméabilité du sol partout sur terre. Et si l'assimilation de données expliquée plus haut permet de remédier partiellement à cela, elle est basée sur l'utilisation de mesures qui par essence comportent des erreurs, instrumentales d'une part et de représentativité d'autre part (pour faire court : on ne mesure pas forcément directement la quantité représentée dans le modèle, et en plus cette mesure n'est ni à un endroit ni à un instant correspondant au maillage du modèle).

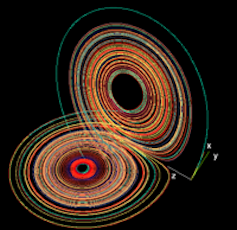
Si l'on ajoute à cela le fameux effet papillon popularisé par Edward Lorenz, c'est-à-dire le fait que, pour certains écoulements ou certaines échelles, une légère différence initiale puisse amener à une situation totalement différente après quelque temps, il y a finalement de quoi être pessimiste quant à la capacité à prévoir de façon fiable. Et pourtant, quoiqu'on en dise dans la file d'attente à la boulangerie ou à la boucherie, la qualité des prévisions est maintenant bien meilleure qu'il y a quelques années, et a fortiori décennies. Soyons honnêtes : si nous râlons aujourd'hui contre une prévision météo, ce n'est pas parce qu'il a plu toute la journée alors que celle-ci était annoncée ensoleillée, mais plus vraisemblablement parce que la pluie est arrivée deux heures plus tôt qu'annoncée, ou que le front de nuages était décalé de 40 kms.

La puissance de calcul et l'IA à la rescousse ?

La précédente litanie des erreurs montre qu'il reste de la marge pour de futures améliorations. Les progrès de l'informatique et le boom de l'intelligence artificielle doivent-ils nous rendre optimistes et nous faire miroiter des lendemains qui, à défaut de chanter, verraient leur météo parfaitement anticipée ? C'est en fait plus compliqué qu'on ne pourrait le croire.

À quoi servent des ordinateurs plus puissants ?

• A utiliser des méthodes numériques plus coûteuses, car plus précises : la solution numérique est alors plus proche de la solution exacte des équations mathématiques. C'est bien, mais comme on l'a vu, ces équations sont incomplètes et cette erreur d'approximation numérique n'est qu'une petite partie du problème.
• A augmenter la « résolution », c'est-à-dire la finesse du maillage. On pourrait alors se dire qu'on va là encore, mécaniquement, diminuer l'erreur d'approximation numérique. C'est vrai… mais le diable se niche dans les détails. En augmentant la résolution, on représente une physique plus riche, de nouveaux phénomènes sont présents, dont certains peut-être mal compris, des rétroactions apparaissent dont on ne soupçonnait pas forcément l'ampleur. Et il faut in fine comprendre tout cela, et peaufiner un nouveau réglage de ce que nous avons appelé la « paramétrisation sous-maille ». Bref, augmenter la résolution est en général encore absolument nécessaire pour les applications dont nous parlons, mais s'accompagne d'un lourd travail de compréhension physique et de réglage avant d'aboutir à un réel gain en précision.
• A mieux quantifier l'incertitude (améliorer l'indice de confiance), en rendant possible de plus nombreuses simulations.

Et l'intelligence artificielle dans tout ça ? On nous explique que l'IA est capable de tout analyser et de tout prédire. Alors, peut-elle aider ici ? A vrai dire, l'apport de l'IA est particulièrement spectaculaire sur des données disparates et/ou concernant des sujets dont le comportement repose sur des lois mal connues, voire inexistantes. Or, pour les fluides géophysiques, les équations mathématiques utilisées actuellement sont d'ores et déjà une bonne représentation de la vraie physique, et l'assimilation de données permet souvent de combiner mesures et modèles de façon quasi optimale. On est donc dans un contexte où l'IA ne doit donc pas être attendue comme le messie. Par contre, elle peut très certainement s'avérer extrêmement utile pour tout ce qui se situe « hors cadre ». Par exemple tout ce qui relève d'une physique encore mal comprise dans ces systèmes de prévision : les interactions complexes entre l'océan et l'atmosphère, la micro-physique, les paramétrisations sous-maille… Les scientifiques saisissent en ce moment tous ces sujets à bras le corps.

Et l'humain dans tout ça ?

N'oublions toutefois pas, dans ce large panorama, un facteur essentiel : le savoir-faire humain, le tour de main du scientifique modélisateur. Les systèmes de prévision sont des mécaniques complexes, et celui-ci les règle minutieusement, et réalise en fait de la « compensation d'erreur ». De la même façon que, pour obtenir une meilleure tarte, on compensera sur le moment la trop grande acidité des fruits à notre disposition en dépassant la quantité de sucre prescrite par la recette, le modélisateur sait adapter son système pour qu'il fournisse les meilleurs résultats possibles. Une conséquence directe en est qu'apporter au système ce qui devrait être une amélioration (une meilleure méthode, une nouvelle paramétrisation…) s'avère souvent décevant au premier abord, voire même détériore la qualité des prévisions. En effet, l'introduction de cette nouveauté met à terre le subtil équilibre des réglages du modèle. Ainsi, quand on pense pouvoir améliorer un élément d'un système de modélisation, le chemin est souvent encore long avant que cela n'améliore les prévisions elles-mêmes, car cela passe par une nouvelle phase de réglages.

En guise de conclusion

Plus que par bonds spectaculaires de lièvre sous EPO, comme ça peut être le cas dans dans certains domaines scientifiques où l'invention d'un nouvel instrument ou d'une nouvelle théorie engendre une véritable révolution, la connaissance et la prévision des milieux géophysiques comme l'atmosphère ou l'océan progressent à petits pas réguliers de tortue : moins romanesque, mais tout aussi efficace sur la durée. A cet égard, l'IA est une nouvelle ressource venant enrichir le panel des outils disponibles. Sans révolutionner la discipline, elle permettra sans nul doute de nouvelles avancées. La tortue poursuit son chemin.

Cet article est republié à partir de The Conversation sous licence Creative Commons. Lire l’article original.

Image de Une : Simulation climatique. Oak Ridge National Laboratory